Modelling Ecosystem Network Structures with Informed and Efficient Parameter Sampling 

Supervisor: Dr Matthew Adams

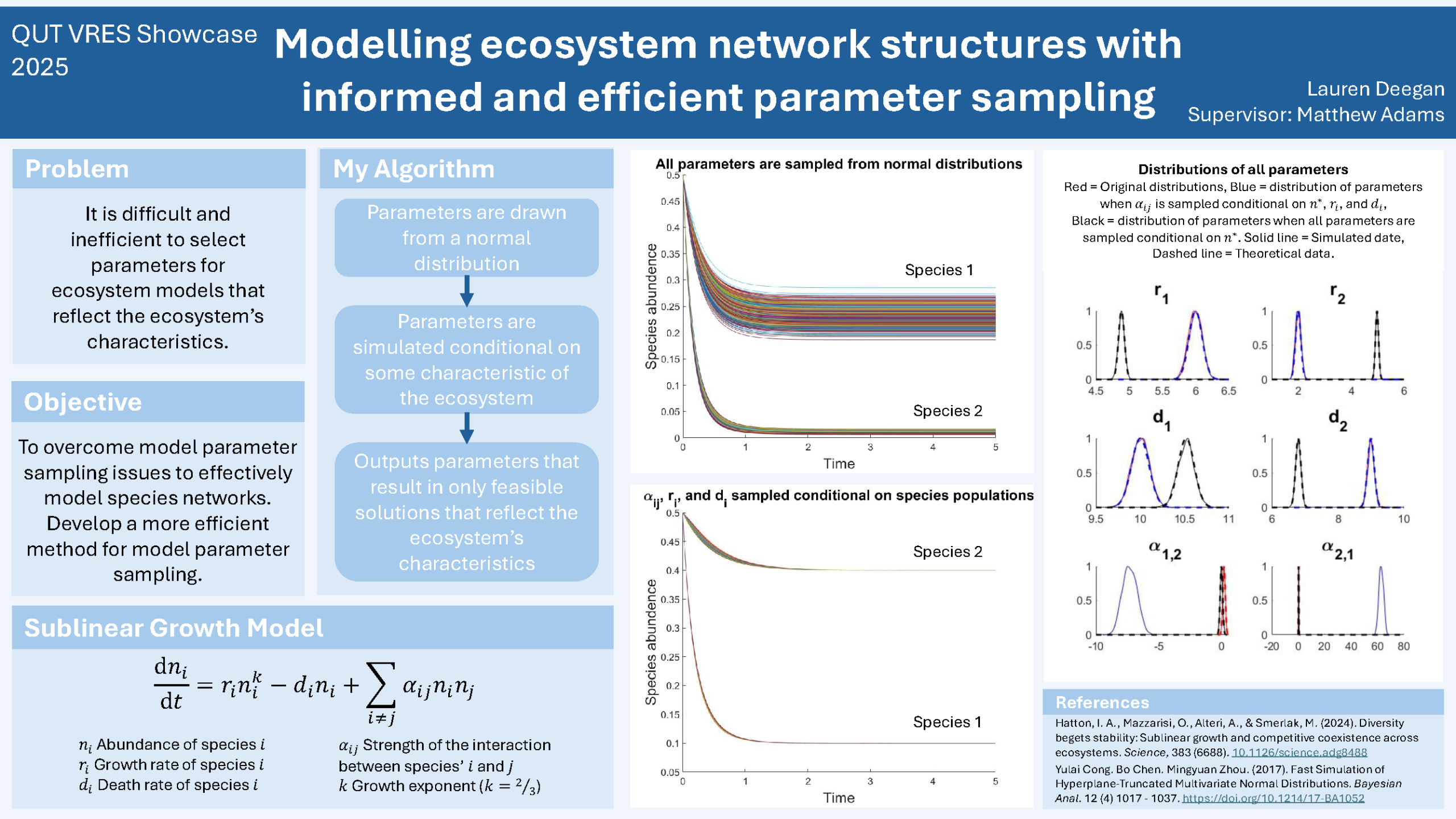
The ability to model and predict the behaviour of diverse ecosystems is an invaluable tool in conservation efforts. One mathematical model proposed recently in the literature for this purpose is the sublinear growth model. This mathematical model can simulate the changes in species populations within ecosystems. A challenge when using the sublinear growth model is the difficulty and inefficiency involved in finding model parameters that lead to feasible solutions. This difficulty is most prevalent when working with large, diverse species networks as the probability of sampling model parameters reflecting the observed ecosystem becomes vanishingly small. The aim of my research was to develop an algorithm that uses more accessible data, such as species abundances, to efficiently find parameters of the sublinear growth model. The parameters were initially drawn from a multivariate Gaussian distribution. I exploited this simplification to analytically derive a method of sampling reasonable model parameters that simultaneously satisfy pre-specified conditions on the species’ populations. This procedure for sampling parameters results in 100% feasible solutions; this contrasts strongly with standard sampling procedures where many infeasible solutions are rejected before feasible parameters can be found. The approach I developed also allows for parameter selection to be informed by the species abundances, which can be more easily estimated by ecologists when compared to direct estimation of model parameter values. This research can be used immediately by environmental scientists to efficiently simulate an ecosystem incorporating their knowledge of species abundances.